中南米音楽の形を見てみたい（１）音楽のカタチって何？

音楽に、形なんてあるの？？？
実は…意外と昔から音楽を幾何学的にとらえようとする研究があったようです。

音楽の要素といえば、

ですね。

これらは、次のようなものですね。

これらを「図」として考えていくために、数学者たちは次のようなところに注目しました。

「戻ってくる」

これを図で表すと、円で表せるんですね。
そして、円と $\mathbb{R}/\mathbb{Z}$ は同相です。

ここで、 $\mathbb{R}/\mathbb{Z}$ は、小数部分が同じだったら同じものとしてみなすようなものです。
例えば、1.5も2.5も0.5も同じということ。

f:id:kyosuu1:20161119231639p:plain

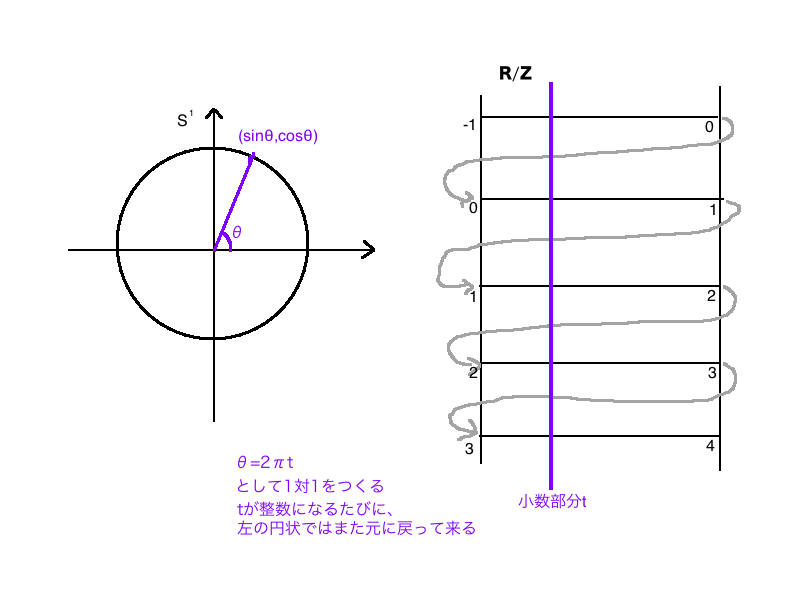
$\mathbb{R}/\mathbb{Z}$ の元は、 $[0,\,1)$ のある元と小数部分が同じものたちを集めてきたものですので、実際計算をするときは $[0,\,1)$ 上で計算してしまいます。

じゃあ、音符をどう $[0,\,1)$ 上にのせるかというとですね…

例えば、
f:id:kyosuu1:20160903072433p:plain
の場合だと、 $\{0, \tfrac{1}{4}, \tfrac{1}{2}, \tfrac{5}{8}, \tfrac{3}{4}\}$ となります。

なぜなら、音階というのは、オクターブ上が2倍で、その間は均等に上がるように（つまり $2^{\frac{1}{12}}$ 倍ずつあがるように）したものだからです。
数学記号で書くと、 $\log _2 f\mod 1$ (ただし、 $f$ は音階の周波数)となります。

f:id:kyosuu1:20161119231743p:plain

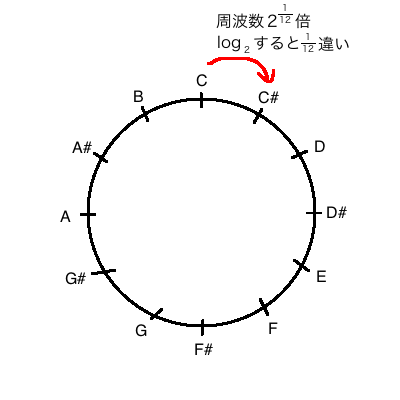
こうしておくことによって、「音符」を、円周上の点としてみなせるようになりました→つまり $[0,\,1)$ 上の点として扱えるようになりました

最初は距離についても少し触れようと思いましたが、やっぱりちゃんと話したいんで次回にします＾＾

渋谷で働くSEのブログ