渋谷で働くSEのブログ

渋谷で働くSEのお粗末なブログです

中南米音楽の形を見てみたい（２）音にも距離があるの？

今回は、音と音の間の「距離」の話をしようと思います。
詳しい内容は

これ([1307.1201] Topology of Musical Data)とか
これ([1602.00739] Towards a topological fingerprint of music)とかを参考にしてください。

えーとですね…

まずリズムにおける距離から。

ボンボを叩いたり、リズムを刻む何かが発生した2つの箇所をa,\,bとして、距離を
d_N(a,\,b) = \min(s,\,1-s)\text{ where } s = |a - b|\mod 1
と定義します。
これは、例えば
f:id:kyosuu1:20160903072433p:plain
こんなリズムの中で、小節内の最後のボンボと最初のボンボとの間の距離を求めるとするならば、
「最初のボンボ」じゃなくて「次の小節の最初のボンボ」考えて距離を求める、ということになります。

実際これに従って距離を求めてみると、最初のボンボと最後のボンボの間の距離は1/4になります。


次に、二つの音（周波数）の距離を考えてみます。

前回、1オクターブは周波数がちょうど2倍になるところで、
オクターブ違いは同じものとして扱いたいという話をしました。

というわけで、二つの周波数 f,\,gについて、音の距離を次のように定義します。

d_{PC}(f,\,g) = \min(s,\,1-s) \text{ where } s = |\log _2 f - \log_2 g| \mod 1

ここで、sと1-sのうち小さい方をとっているのは、例えばこんなやつを同じものとしてみなしたいからです。
例えば、「ドレ」と「ドラ＃」とか。
後者って、ドを1オクターブあげて「ラ＃ド」にしちゃうと、「ドレ」と同じ長２度となるんですね。
このような操作をするために設けているのが1-sなんです。

そして、ハーモニーの距離は、上で定義した距離を用いて次のように表します。
ハーモニーf = (f_1,\,f_2,\,\cdots,\,f_n),\,g = (g_1,\,g_2,\,\cdots,\,g_n)について、距離を

d_{CC}(f,\,g) = \min \displaystyle\sum _{i=1} ^{n} d_{PC} (f_i,\,\sigma(g_i)),

(ただし\sigmaはサイズnの順列すべて)と定めます。

fは固定していて、gの中の音たちが入れ替わってるような感じですね。

例えば、 f = (\text{ド, ミ, ソ}),\,g=(\text{ミ, ソ, ド})
(ドとかミとかソとかは、適当なところの周波数だと思ってください)
の距離を求めるのであれば、fはそのままにし、gの中の音たちは1オクターブ上とか下とかに動かしてみるわけですね。

このとき、gの中の「ド」を一番はじめに持って来ると、fと一致しますね。

コート(chord)というのは、根音が違っても構成している音がすべて同じであれば同じものとみなせるので、それを実現するために「最小値」を取っているということです。

数式をあまり入れたくなかったんですが、数式なしでは説明がしづらかったです。

次回は、実際Rでpersistent homologyを求めてみようと思います。

中南米音楽の形を見てみたい（１）音楽のカタチって何？

音楽に、形なんてあるの？？？
実は…意外と昔から音楽を幾何学的にとらえようとする研究があったようです。

音楽の要素といえば、

  • メロディ
  • ハーモニー
  • リズム

ですね。

これらは、次のようなものですね。

  • メロディ : 時間によって変わっていく音たちの集まり
  • ハーモニー : 同じ時間に同時になっている音たち
  • リズム : 時間の刻み方


これらを「図」として考えていくために、数学者たちは次のようなところに注目しました。

  • 音階は、周波数が2倍になると「元」に戻ってくる
  • リズムは、1小節分が繰り返される

「戻ってくる」

これを図で表すと、円で表せるんですね。
そして、円と\mathbb{R}/\mathbb{Z}は同相です。

ここで、\mathbb{R}/\mathbb{Z}は、小数部分が同じだったら同じものとしてみなすようなものです。
例えば、1.5も2.5も0.5も同じということ。

f:id:kyosuu1:20161119231639p:plain

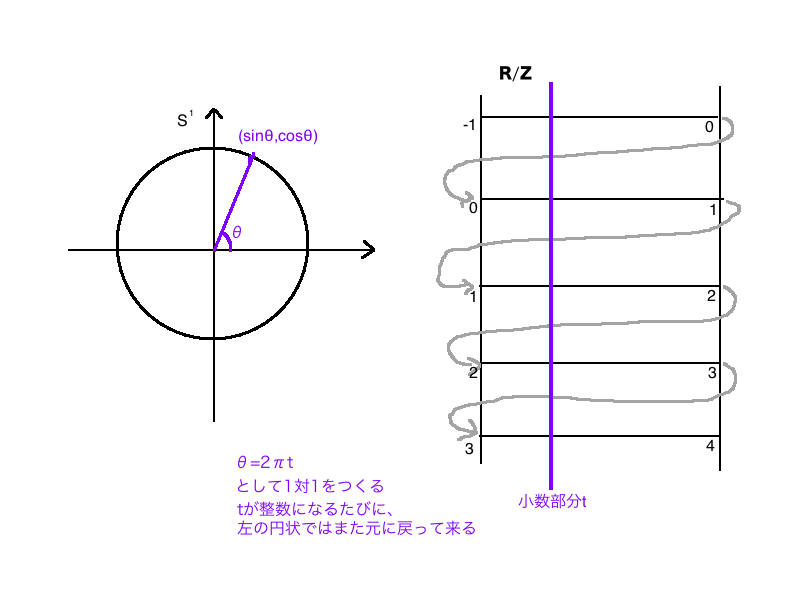
\mathbb{R}/\mathbb{Z}の元は、[0,\,1)のある元と小数部分が同じものたちを集めてきたものですので、実際計算をするときは[0,\,1)上で計算してしまいます。

じゃあ、音符をどう[0,\,1)上にのせるかというとですね…

  • リスムの場合は、1小節を1とし、音符の位置を割合で表す。

例えば、
f:id:kyosuu1:20160903072433p:plain
の場合だと、\{0, \tfrac{1}{4}, \tfrac{1}{2}, \tfrac{5}{8}, \tfrac{3}{4}\}となります。

  • 音階は、周波数の \log _2をとってから、小数部分をとります。

なぜなら、音階というのは、オクターブ上が2倍で、その間は均等に上がるように（つまり 2^{\frac{1}{12}}倍ずつあがるように）したものだからです。
数学記号で書くと、 \log _2 f\mod 1 (ただし、 fは音階の周波数)となります。

f:id:kyosuu1:20161119231743p:plain

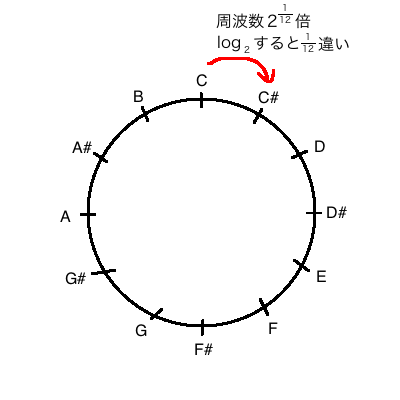
こうしておくことによって、「音符」を、円周上の点としてみなせるようになりました→つまり [0,\,1)上の点として扱えるようになりました

最初は距離についても少し触れようと思いましたが、やっぱりちゃんと話したいんで次回にします＾＾

InterBEEに行きました

AI 人工知能

昨日はInterBEE(放送機器展)に行ってきました。

いろんな放送機器やVR機材、音響機材がたくさん展示されていました。

 

まず、うちの会社のやつはこちら。


f:id:kyosuu1:20161117223334j:image

 

悲しいことに、顔を見つけては全部隠してくれてます（笑）

なかなかシュールですね。

 

そしてすごかったやつが…

こちら!

f:id:kyosuu1:20161117223456j:image

ノイズのところを選ぶと、ノイズが消えます。

平坦化してるのかな…たぶん。

 

そして…動作のトラッキングをしてくれるやつもありました。


f:id:kyosuu1:20161117223716j:image

スポーツ中継用みたいですね。

 

音声を認識して字幕を作ってくれるやつもありました。ここまで音声認識技術が発展するとは…
f:id:kyosuu1:20161117223752j:image

 

最後に、幕張メッセのきれいなイルミネーション。


f:id:kyosuu1:20161117223921j:image


f:id:kyosuu1:20161117223932j:image

日が完全に暮れていない中途半端な時間帯の方が完全に暗くなったときより写メとるにはいい気がします。

 

私の報告は以上です🙋

本田式認知特性

雑談

会社でなぜか本田式認知特性（４０問バージョン）が流行りました。

テストツールはこちら。

 

私の結果はこんな感じです。

f:id:kyosuu1:20161113010507p:plain

 

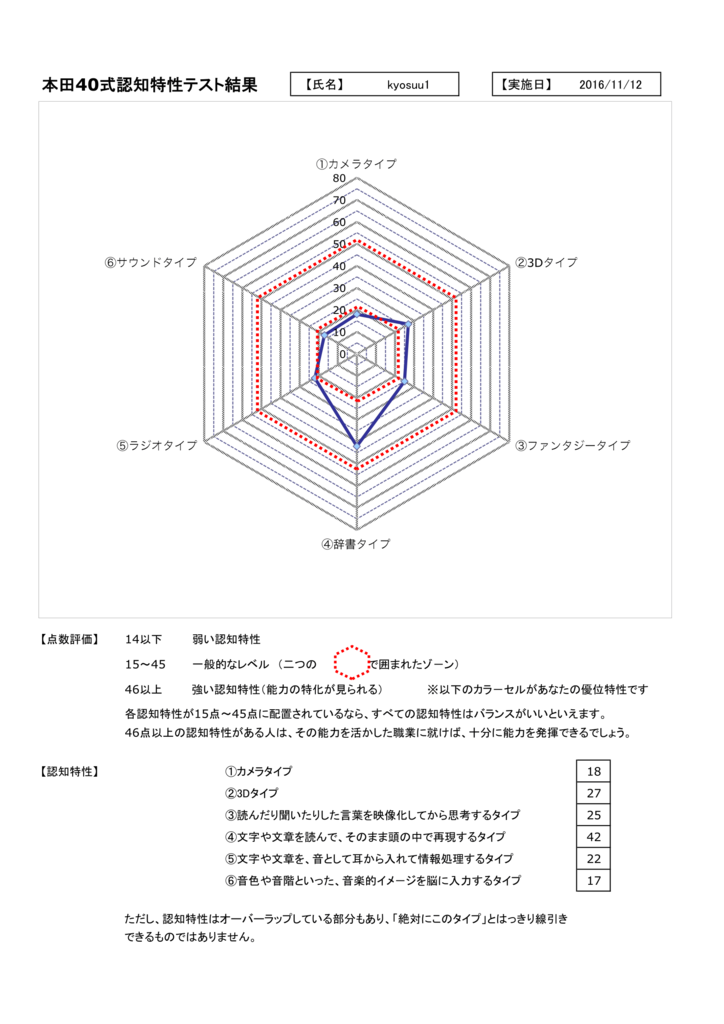
「特化」までにはいってないんですが、私はどうも文字に強いらしいです。

大学時代も、全般的にできがいい方だったのに、なぜか幾何学だけ特に苦手でした。

代数と解析は得意な方でした。特に、式をいじるのが好きで、大学1年のときは微積分が好きでした。

 

会社のみなさんは、それぞれ結果が違っていて面白かったです。

それぞれ違うみんなと一緒に働けて、本当に恵まれた環境だな、と思いました＾＾

 

ちなみに、私は人より独学が得意らしいです。

中1の頃から独学で先取り学習をしていました。

ただ数学が好きになっちゃったから。

 

中2の頃には、すでに中学校の全過程をしっかり理解していました（人に教えられるレベルに達していた）

 

私が中1の頃といえば、まだうちのネットがモデムだった時代で、宿題をやるにしても親の顔色を伺いながらやってた頃です。

mp3のダウンロードには1時間かかってました。

 

そんな環境の中だったので、ネット講座というアイデアなんかそもそもありませんでしたし…（今のようなe-learning環境が整ってきたのはだいたい高校生のときぐらい）

 

そんな中で頑張れたのは、私が文字に強いからだったらしいです。

その反面、講義は、知ってる内容じゃないとついていけないという弱点もあったりします。

そんなときってだいたい眠くなっちゃうので、講演者には申し訳ないばかりですが。

 

まあ、今日はちょっと雑談でしたー

TOEIC Speaking & Writing 受けてきました

英語 外国語 資格

数年前、就活を目前にして焦って受けようとしていたTOEIC Speaking & Writing。

寝坊して受けられませんでした⤵⤵

 

今回は寝坊なんかするまい!遅刻なんかするまい!

と思い、午後受験することにし、早めに会場付近まで行きました。

 

そしていよいよ本番…

みんなはすらすら答えてます。しっかり練習しておいたようです。

私は…うむ、スピーキングは前述の通り練習しておりません。当然しゃべれるわけがないです。

 

そしてライティング。

こっちは頑張ってなんとか書きました。

問題集より書きやすかった感じです。

そして、直前に必須表現をざっとみといたのがちょっと役に立った気がします。

 

今度は、まず日本語で考え、それを英語に直す練習をするひつようがあるのでは、と思います。

 

問題形式そのものが、

「xxについて300字以上で意見をのべなさい」とか、

「２つの情報と１つの質問を入れて次のメール（めっちゃ短い）に答えなさい」

みたいな感じなので、実際日本語で答えろといってもちょっと時間が必要かもしれないです。

 

いきなり考えようとしても、日本語ですらぱっぱっと考えられない問題がけっこうあるので、

頭の体操をしておかないといけないのでは、と思いました。

英語の難しさといえばやっぱり前置詞

外国語 英語

英語が難しい理由といえば…

やっぱ前置詞ですね。

 

英語の動詞には、自動詞と他動詞だけがあると思ったら大間違いです。

私は、こう思ったほうがいいのではないかと思いました。

 

1. 日本語でも英語でも自動詞：「起こる」「現れる」など

2. 日本語では他動詞だが、英語だと前置詞付きでやっと他動詞になる動詞：「卒業する(graduate from)」、「見る(look at)」など

3. 日本語でも英語でも他動詞：「探す(find)」など

4. 日本語だと自動詞か他動詞か微妙だが、英語だと他動詞：「議論する(discuss)」など

→discussの後ろにはaboutがつかない

→実は博論書くときにここ間違えてたりした

5. そもそも品詞が違う：「好き(like)」など

 

私はこう考えて勉強していて、2番目の動詞を覚えるときは必ず前置詞を一緒に覚えるようにしています。

逆に、4番目のような動詞を覚えるときは、「この動詞は助詞込みだな」と覚えるようにしています。

 

まだまだこの方法は只今試している最中です。

覚える量はたしかに多くなります。

しかし、数こなせば、時間をかけてじっくりやっていけばいずれは身につくだろうと思ってやってます。

 

今年度は「作文の期間」です。

スピードは全く気にしません。

時間かけても正しい文を書くことが今年度の目標です。

なので、TOEIC speaking&writingの勉強も、今年度はwritingの勉強しかしていません。

スピードを上げることは、来年度からやろうと思います。

 

今年度は

＞単語や熟語をためる

＞ライティングの練習を通して正確度を上げる

＞話すときは随時文法をチェックしながらゆっくりでも正しく言おうとする

ように心がけています。

 

「言う」「書く」ことはもちろん大事です。

しかし、人に信頼され、中身をきちんとみてもらうためには「正しく」言ったり書いたりする必要があります。

なので、ちょっと複雑そうに見えてもゆっくり、きちんとやったほうがいいと思っています。

 

明日いよいよ待ちに待ったTOEIC speaking & writingです。

状況を全部知っているわけでもないのに「返事しろ」という問題なんて無茶だな、という印象しかないですが…

とりあえず頑張ります！

位相的データ分析(TDA)にハマってます

AI 人工知能

次の自主研究の課題を

「コード(chord)が書いてあるテキストファイルを解析し、新しいコードを作成する」

と設定し、基本情報ギジュ者試験が終わり次第着手しようと思っていました。

 

しかし…

今は、「位相的データ分析」(Topological Data Analysis)に完全にハマっています。

 

位相的データ分析は何かというと、

データを「点」としてみなし、それらをどんどんつなげていきながら形を見ていくようなものです。

 

ちょうど、高分子の物質や結晶が、原子同士で繋がっている構造をしていることから、

原子一つ一つを点とみなして、その点からつくられる図形の変化を見るという研究が盛んに行われているそうです。

 

応用分野としては、今は医療系・生物系・化学系が多いみたいですね。

 

画像処理・自然言語処理・音楽分析などといった分野の論文も出てます。

しかし、まだそこまで多くもないような気が…

 

一応音楽のTDAにはちょっと興味あります。

やっぱまたSan JuanitoとTobasを分析してみるとなんか面白いのが見えるんじゃないかな…とか思ったり。

でもまだ論文読んでなかったりします、実はw

 

 

詳しい説明はしません。

リンクだけ貼っときます。

 

1. すっごい参考になった本

タンパク質構造とトポロジー ―パーシステントホモロジー群入門― (シリーズ・現象を解明する数学)

タンパク質構造とトポロジー ―パーシステントホモロジー群入門― (シリーズ・現象を解明する数学)

 

 

2. 結晶分析

www.jst.go.jp

 

3. クラインボトル

http://math.uchicago.edu/~shmuel/AAT-readings/Data%20Analysis%20/mumford-carlsson%20et%20al.pdf

 

（これを理解するためには、

https://dash.harvard.edu/bitstream/handle/1/3637108/Mumford_NonlinStatPatches.pdf?sequence=1 これも一緒に読んでおくといいです）

 

4. 自然言語処理

http://pages.cs.wisc.edu/~jerryzhu/pub/homology.pdf

 

5. 音楽

https://arxiv.org/abs/1307.1201

 

だいたいこんな感じですかね…

 

応用先とかは…

経験の浅い私にはまだ思いつかないので…

とりあえず音楽とか、タンパク質の構造とか見てみようと思います。

 

これを書きながらまた調べて見ると、

画像のノイズを取り除くのに応用されているみたいですので、

そこらへんもちょっと調べてみようかと思います。

 

あと、音楽のpersistent homologyもちょっと覗き見できたらいいですね。